Matematika/Trikampiai

Trikampis

Trikampiu vadiname figūrą, kurią sudaro trys taškai, nepriklausantys vienai tiesei, ir trys atkarpos, jungiančios kiekvienus du iš tų taškų. Tuos tris taškus vadiname trikampio viršūnėmis, o atkarpas jo kraštinėmis.

Trikampį žymime nurodydami jo viršūnes:

Trikampio ABC kampu prie viršūnės A vadiname kampą, kurį sudaro pustiesės AB ir AC. Panašiai apibrėžiami to trikampio kampai prie viršūnių B ir C.

Trikampio aukštine vadiname statmenį, išvestą iš trikampio viršūnės į tiesę, kurioje yra prieš viršūnę esanti kraštinė. BD yra trikampio aukštinė:

Trikampio pusiaukampine vadiname trikampio kampo pusiaukampinės atkarpą, kuri dalija kampą pusiau ir jungia trikampio viršūnę su prieš ją esančios kraštinės tašku:

Trikampio pusiaukraštine vadiname trikampio kampo pusiaukraštinės atkarpą, kuri dalija kraštinę pusiau bei jungia trikampio viršūnę su prieš ją esančios kraštinės viduriu:

Trikampio vidurine linija vadiname atkarpą, kuri jungia dviejų jo kraštinių vidurio taškus.

$DE$ – vidurinė linija. $DE={\frac {1}{2}}AC$

Trikampio lygumas

Lygiomis atkarpomis vadiname atkarpas, kurios yra vienodo ilgio. Lygiais kampais vadiname kampus, kurie yra vienodo laipsninio mato.

Yra trys trikampių lygumo požymiai:

1. Trikampių lygumo požymis pagal dvi kraštines ir kampą tarp jų.
2. Trikampių lygumo požymis pagal kraštinę ir prie jos esančius kampus.
3. Trikampio lygumo požymis pagal tris kraštines.

Trikampio perimetras

Trikampio perimetras yra visų trikampio kraštinių ilgių suma.

$P=a+b+c\,$

Trikampio pusperimetris lygus pusei perimetro.

$p={\frac {P}{2}}={\frac {a+b+c}{2}}$

Trikampio kampų suma lygi 180°

Trikampio pusiaukraštinės

Iš trikampio kampo išėjusi tiesė, kuri priešais tą kampą esančią kraštinę dalina pusiau, vadinama trikampio pusiaukraštinė. Jei susikerta dvi trikampio pusiaukraštinės, tai jos vieną kita padalina santykiu 2:1. T. y. viena trikampio pusiaukraštinė, kitą trikampio pusiaukraštinę dalina santykiu 2:1. Didesnė padalintos pusiaukraštinės dalis yra arčiau kampo.

Trikampio ploto radimas žinant koordinates

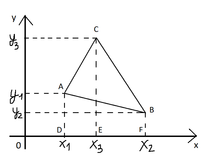
11 pav.

Trikampio plotas. Bet kokiems taškams $A(x_{1};y_{1})$, $B(x_{2};y_{2})$ ir $C(x_{3};y_{3})$ negulintiems ant vienos tiesės, plotas S trikampio ABC išreiškiamas formule

$S={\frac {1}{2}}|[(x_{2}-x_{1})(y_{3}-y_{1})-(x_{3}-x_{1})(y_{2}-y_{1})]|.$

Įrodymas. Plotą trikampio ABC pavaizduotą pav. 11, galima rasti taip:

$S_{ABC}=S_{ADEC}+S_{BCEF}-S_{ABFD},\;$

kur $S_{ADEC}$, $S_{BCEF}$, $S_{ABFD}$ - plotai atitinkamų trapecijų.

Kadangi

$S_{ADEC}=|DE|{\frac {|AD|+|CE|}{2}}={\frac {(x_{3}-x_{1})(y_{3}+y_{1})}{2}},$

$S_{BCEF}=|EF|{\frac {|EC|+|BF|}{2}}={\frac {(x_{2}-x_{3})(y_{2}+y_{3})}{2}},$

$S_{ABFD}=|DF|{\frac {|AD|+|BF|}{2}}={\frac {(x_{2}-x_{1})(y_{1}+y_{2})}{2}},$

įstatę išraiškas šiems plotams į lygybę $S_{ABC}=S_{ADEC}+S_{BCEF}-S_{ABFD},$ gausime formulę

$S_{ABC}=S_{ADEC}+S_{BCEF}-S_{ABFD}={\frac {1}{2}}|[(x_{3}-x_{1})(y_{3}+y_{1})+(x_{2}-x_{3})(y_{2}+y_{3})-(x_{2}-x_{1})(y_{1}+y_{2})]|=$

$={\frac {1}{2}}|[(x_{1}-x_{2})(y_{1}+y_{2})+(x_{2}-x_{3})(y_{2}+y_{3})+(x_{3}-x_{1})(y_{3}+y_{1})]|=$

$={\frac {1}{2}}|(x_{1}y_{1}+x_{1}y_{2}-x_{2}y_{1}-x_{2}y_{2}+x_{2}y_{2}+x_{2}y_{3}-x_{3}y_{2}-x_{3}y_{3}+x_{3}y_{3}+x_{3}y_{1}-x_{1}y_{3}-x_{1}y_{1})|=$

$={\frac {1}{2}}|(x_{1}y_{2}-x_{2}y_{1}+x_{2}y_{3}-x_{3}y_{2}+x_{3}y_{1}-x_{1}y_{3})|={\frac {1}{2}}|x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})|=$

$={\frac {1}{2}}|(x_{2}-x_{1})(y_{3}-y_{1})-(x_{3}-x_{1})(y_{2}-y_{1})|.$

Pavyzdis. Duoti taškai A(1; 1), B(6; 4), C(8; 2). Rasti trikampio ABC plotą. Randame:

$S_{ABC}={\frac {1}{2}}|[(x_{2}-x_{1})(y_{3}-y_{1})-(x_{3}-x_{1})(y_{2}-y_{1})]|={\frac {1}{2}}|(6-1)(2-1)-(8-1)(4-1)|={\frac {1}{2}}|5\cdot 1-7\cdot 3|={\frac {1}{2}}|5-21|={\frac {1}{2}}|-16|={\frac {16}{2}}=8;$

$S_{ABC}=S_{ADEC}+S_{BCEF}-S_{ABFD}={\frac {1}{2}}|x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})|={\frac {1}{2}}|1(4-2)+6(2-1)+8(1-4)|={\frac {1}{2}}|2+6+8\cdot (-3)|=$

$={\frac {1}{2}}|8-24|={\frac {1}{2}}|-16|=8.$