Matematika/Diferencialas

Iš Wikibooks.

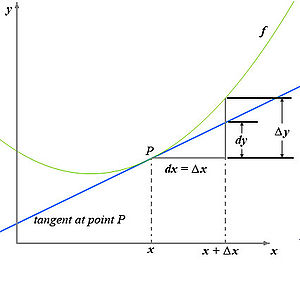
Funkcija (žalia kreivė) ir jos diferencialas taške P (mėlyna tiesė)

Diferencialas - funkcijos pokyčio tiesinė pagrindinė dalis. Funkcija y = f(x), apibrėžta intervale (a, b), vadinama diferencijuojamąja taške x $_{\in}$ (a, b), jei jos pokytį Δy = f(x + Δx) - f(x) galima išreikšti dviejų dėmenų suma: Δy = AΔx + o(Δx); čia A - skaičius, nepriklausantis nuo Δx.

Pavyzdžiui, yra funkcija f(x)=x². Tos funkcijos išvestinė yra $\frac{f(x+\Delta x)-f(x)}{\Delta x}=\frac{(x+\Delta x)^2-x^2}{\Delta x}=$ $=\frac{x^2+2x\Delta x+(\Delta x)^2-x^2}{\Delta x}=\frac{2x\Delta x+(\Delta x)^2}{\Delta x}=2x+\Delta x$

$y'=f'(x)=\frac{dy}{dx}=\lim_{\Delta x \to 0}2x+\Delta x=2x.$

Įstatykime vietoje x kokią nors reikšmę, pavyzdžiui, x=3.

Δy = AΔx + o(Δx) = 2xΔx + (Δx)²=6Δx + (Δx)²,

čia A = 2x = 6 = f'(x); o(Δx) = (Δx)².

Taigi funkcijos pokytis yra Δy = f(x + Δx) - f(x) = AΔx + o(Δx), o diferencialas dy = AΔx = y'Δx = y'dx = f'(x)dx; Δx = dx.

Turinys

1 Sumos, skirtumo, sandaugos ir dalmens diferencijavimo taisyklės
2 Sudetinės funkcijos diferencijavimas
3 Sudetinės laipsninės funkcijos diferencijavimas
4 Diferencialinių lygčių sprendimas
5 Susiję straipsniai

[redaguoti] Sumos, skirtumo, sandaugos ir dalmens diferencijavimo taisyklės

Sumos diferencijavimas.

[u (x) + v (x)]' = u'(x) + v'(x)

[u (x) - v (x)]' = u'(x) - v'(x)

Sandaugos diferencijavimas.

[u (x) v (x)]' = u'(x) v (x) + u (x) v'(x)

Dalmens diferencijavimas.

$[\frac{u(x)}{v(x)}]'=\frac{u'(x)v(x)-u(x)v'(x)}{v^2(x)}$

[redaguoti] Sudetinės funkcijos diferencijavimas

$f'(g(x)) = f'(t) g'(x),\, t=g(x)$

Pavyzdžiui,

f (x) = (x 2 + 1) 3

,

kur $f'(t) = (t 3)'$ ; $g'(x) = (x 2 + 1)'$ .

f'(x) = f'(t) g'(x) = (t 3)'(x 2 + 1)' = 3 t 22 x = 3(x 2 + 1) 22 x

.

Pavyzdys iš trigonometrijos,

$f(x) = \sin(x^2),\,$

f'(t) = (sin(t))'

g'(x) = (x 2)'

f'(x) = f'(t) g'(x) = (sin(t))'(x 2)' = 2 x cos(t) = 2 x cos(x 2)

.

[redaguoti] Sudetinės laipsninės funkcijos diferencijavimas

$f(x)=g(x)^{h(x)}=e^{\ln g(x)^{h(x)}}=e^{h(x)\ln g(x)},$

$f'(x)=(g(x)^{h(x)})'=(e^{h(x)\ln g(x)})'=e^{h(x)\ln g(x)}(h(x)\ln g(x))'=g(x)^{h(x)}\cdot(h(x)\ln g(x))'.$

$(g(x)^{h(x)})'=g(x)^{h(x)}\cdot (h'(x)\ln g(x)+h(x)\frac{g'(x)}{g(x)}).$

Pavyzdžiai

$((3x^4)^{5x^3})'=((3x^4)^{5x^3})(15x^2\ln(3x^4)+5x^3\cdot\frac{12x^3}{3x^4}).$

$((3x^2+2x+5)^{8x^3+2x^2 +4})'=$

$=(3x^2+2x+5)^{8x^3+2x^2 +4}((24x^2+4x)\ln(3x^2+2x+5)+(8x^3+2x^2 +4)\frac{6x+2}{3x^2+2x+5}).$

$((\sin x)^{\cos x})'=(\sin x)^{\cos x}(\frac{\cos^2 x}{\sin x}-\sin x\ln\sin x).$

$(\sqrt{\frac{3x+5}{4x+7}})'=\sqrt{\frac{3x+5}{4x+7}}\cdot (\frac{1}{2}(\ln(3x+5)-\ln(4x+7)))'=\sqrt{\frac{3x+5}{4x+7}}\cdot \frac{1}{2}(\frac{3}{3x+5}-\frac{4}{4x+7}).$

$(x^{\frac{1}{x}})'=x^{\frac{1}{x}}\cdot (\frac{1}{x}\ln x)'=x^{\frac{1}{x}}\cdot(-\frac{1}{x^2}\ln x+\frac{1}{x}\cdot \frac{1}{x})=x^{\frac{1}{x}}\cdot \frac{1-\ln x}{x^2}.$

[redaguoti] Diferencialinių lygčių sprendimas

$y'={y\over x},$

${dy\over dx}={y\over x},$

${dy\over y}={dx\over x},$

$\int{dy\over y}=\int{dx\over x},$

ln | y | = ln | x | + | C 1 | ,

| y | = | C 1 | | x | ,

$y=\pm C_1 x,\;\pm C_1=C,$

y = C x .

$y'=-{y\over x},$

${dy\over dx}=-{y\over x},$

${dy\over y}=-{dx\over x},$

$\int{dy\over y}=-\int{dx\over x},$

$\ln|y|=-\ln|x|+\ln|C_1|=\ln|{C_1\over x}|,$

$|y|={|C_1|\over |x|},$

$y=\pm {C_1\over x}={C\over x}.$

$y'=3y^{2\over 3},$

${y'\over 3y^{2\over 3}}=1,$

${{dy\over dx}\over 3y^{2\over 3}}=1,$

${dy\over 3y^{2\over 3}}=dx,$

$\int{dy\over 3y^{2\over 3}}=\int dx,$

${1\over 3}\int y^{-{2\over 3}}dy=\int dx,$

${1\over 3}\cdot {y^{1\over 3}\over {1\over 3}}=x+C,$

$y^{1\over 3}=x+C,$

y = (x + C) 3 .

$y' - 2 x y 2 + 5 = 0,$

${dy\over dx}=2xy^2-5,$

$\int dy=\int(2xy^2-5)dx,$

y = x 2 y 2 - 5 x + C .

$(1 + x) y d x + (1 - y) x d y = 0,$

${1+x\over x}dx+{1-y\over y}=0,$

$\int({1\over x}+1)dx+\int({1\over y}-1)dy=\int 0 dx,$

ln | x | + x + ln | y | - y = C,

ln | x y | + x - y = C .

$y' x - x 2 - y = 0,$

${dy\over dx}=x+{y\over x},$

$\int dy=\int(x+{y\over x})dx,$

$y={x^2\over 2}+y\ln|x|+C;$

y = x 2 + C x .

$(x 2 y + y) d x + (x 2 - x 2 y) d y = 0,$

y (x 2 + 1) d x = x 2 (y - 1) d y,

${1+x^2\over x^2}dx={y-1\over y}dy,$

$\int({1\over x^2} +1)dx=\int (1-{1\over y})dy+C,$

$x-{1\over x}-y+\ln|y|=C.$

$y'=2\sqrt{y},$

${dy\over dx}=2\sqrt{y},$

${dy\over 2\sqrt{y}}=dx,$

${1\over 2}\int{dy\over \sqrt{y}}=\int dx,$

${1\over 2}\cdot{\sqrt{y}\over {1\over 2}}=x+C,$

$\sqrt{y}=x+C,$

y = (x + C) 2 .

$y' = x (y 2 + 1),$

${dy\over y^2+1}=xdx,\;y^2+1\neq 0,$

$\arctan y={x^2\over 2}+C,$

$y=\tan({x^2\over 2}+C),\;-{\pi\over 2}<{x^2\over 2}+C<{\pi\over 2} .$

$y'={1+y^2\over 1+x^2},$ kai $y (1) = 0,$

${dy\over 1+y^2}={dx\over 1+x^2},$

arctan y = arctan x + C,

arctan0 = arctan1 + C,

$\arctan y=\arctan x-{\pi\over 4},$

arctan y = arctan x - arctan1,

$\arctan y=\arctan{x-1\over 1+x\cdot 1},$

$y={x-1\over x+1}.$

$x y' + y = 0,$ $y | x = 3 = 2;$

$x{dy\over dx}=-y;$

${dy\over y}=-{dx\over x};$

ln | y | = - ln | x | + ln | C | ;

$y={C\over x};$

$2={C\over 3};$

C = 6;

$y={6\over x}.$

$y'-{2xy\over 1+x^2}=0,$

${dy\over dx}={2xy\over 1+x^2},$

$\int {dy\over y}=\int{2x\over 1+x^2}dx,$

$\int {dy\over y}=\int{d(1+x^2)\over 1+x^2},$

ln | y | = ln | 1 + x 2 | + ln | C | ,

y = C (1 + x 2).

Uždavinys apie radiaktyvųjį skilimą. Bandymais nustatyta, kad radioaktyviosios medžiagos skilimo greitis proporcingas nesuskilusios medžiagos kiekiui. Nustatykime nesuskilusios medžiagos kiekio m priklausomybę nuo laiko t, kai pradinis medžiagos kiekis lygus $m 0 .$

Sprendimas. Radioaktyvios medžiagos skilimo greitis lygus ${dm\over dt}.$

Pagal sąlyga,

${dm\over dt}=-km;\;(1)$

čia $k > 0$ - proporcingumo koeficientas. Kadangi radioaktyviosios medžiagos kiekis ilgainiui mažėja, tai ${dm\over dt}<0,$ todėl (1) lygties dešinėje pusėje rašome minuso ženklą.

${dm\over m}=-k\;dt,$

$\int{dm\over m}=-k\int dt,$

$\ln m=-kt+\ln C.\;(2)$

(Norėdami supaprastinti bendrojo sprendimo išraišką, vietoje C rašome $ln C$ ).

$\ln m-\ln C=\ln{m\over C}=-kt,$

$e^{\ln{m\over C}}={m\over C}=e^{-kt},$

$m=Ce^{-kt}.\;(3)$

Uždavinio sąlygoje nurodyta, kad laiko momentu

t = 0

pradinis medžiagos kiekis lygus

m 0 .

Šios sąlygos yra pradinės ir trumpai užrašomos taip:

m | t = 0 = m 0 .

Į (3) reiškinį įrašę vietoje m dydį $m 0$ , o vietoje t - nulį, gauname: $m_0=Ce^{-k\cdot 0}=C.$ Taigi iš bendrojo sprendinio išplaukia toks sprendinys

m = m 0 e - k t,

(4)

atitinkantis duotąsias pradines sąlygas.

Radiaktyvios medžiagos skilimo greitį apibūdina pusamžio, arba pusėjimo trukmės, sąvoka. Taip vadinamas laikas T, per kurį suskyla pusė pradinio radiaktyvios medžiagos kiekio. Į (4) lygybę įrašę $m={m_0\over 2}$ ir

t = T,

gauname sąryšį

${1\over 2}m_0=m_0 e^{-kT},$

${1\over 2}=e^{-kT},$

$\ln{1\over 2}=-kT,$

ln1 - ln2 = - k T,

$\ln 2 - \ln 1=\ln{2\over 1}=\ln 2=kT.$

Taigi koeficientą k su skilimo pusamžiu T sieja sąlyga

$k={\ln 2\over T}.$

Tuomet atskirasis diferencialinės lygties sprendinys, iš lygties (4), užrašomas taip:

$m=m_0 e^{-t{\ln 2\over T}}.$

Puamžio T reikšmės nustatomos eksperimentais. Įvairių radioaktyviųjų medžiagų skilimo pusamžio reikšmės yra labai skirtingos (žr. lentelę).

Radiaktyvioji medžiaga	Anglis - 14	Plutonis - 244	Radis - 226	Stroncis - 90	Uranas - 235	Uranas - 238
Skilimo pusamžis	5730 metų	$8\cdot 10^7$ metų	1575 metų	28.1 metų	$7.07\cdot 10^8$ metų	$4.51\cdot 10^9$ metų

Iš lygties (4), koeficientas k nustatomas iš stebėjimų. Tegu per laiką $t 0$ skyla a% radiaktyviosios medžiagos nuo pradinės masės $m 0 .$ Tenkinama sąlyga

$(1-{a\over 100})m_0=m_0 e^{-kt_0},$

$(1-{a\over 100})= e^{-k t_0},$

$\ln(1-{a\over 100})= -k t_0,$

$k=-{1\over t_0}\ln(1-{a\over 100}).$

Tokiu budu buvo nustatyta, kad Radžiui $k = 0.00044$ (laiko matavimo vienetas - metas).

Įstatę šią reikšmę į formulę (4), gauname:

m = m 0 e - 0.00044 t .

Rasime periodą pusės suskilimo radžio, t. y. laiko tarpą, per kurį suskyla pusė pirminės masės radžio. Įstatę (4) formulę vietoje m reikšmę ${m_0\over 2},$ gausime lygtį pusamžio T nustatymui:

${m_0\over 2}=m_0 e^{-0.00044T},$

- ln2 = - 0.00044 T,

$T={\ln 2\over 0.00044}={0.69314718\over 0.00044}\approx 1575$ metų.

Raketos uždavinys. Raketa su pradine mase $M 0$ juda tiesiaeigiai dėl nenutrukstamo dujų išmetimo išmetamų iš raketos. Greitis $u 0$ išmetamų dujų (raketos atžvilgiu) pastovus ir nukeiptas į priešingą raketos judėjimo kryptį su pradiniu greičiu $v 0$ . Rasime dėsnį raketos judėjimo nepaisydami gravitacijos ir oro pasipriešinimo.

$M{dv\over dt}=-u_0{dM\over dt}.$

Čia ${dM\over dt}=\mu$ - išnaudojama masė degalų per sekundę, esant nekintamam degalų degimui

μ = c o n s t

, M - kintanti masė raketos.

$dv=-u_0{dM\over M},$

v = - u 0 ln M + C .

Konstantą C randame iš sąlygos

v = v 0

,

M = M 0,

kai

t = 0

,

C = u 0 ln M 0 + v 0,

ir todėl

$v=u_0\ln{M_0\over M}+v_0.$

Pavyzdžiui, jeigu norima akseleruoti raketą iki šviesos greičio, kai raketos masė su kuru lygi $M_0=10000\; (kg),$ o raketos masė be kuro lygi $m={M_0\over 2}=5000\;(kg),$ tai kuras sveria pusė raketos masės. Viso išmesto raketos kuro energija, sakykim, anihiliacijos metu yra $E_0={M_0\over 2}c^2 =5000\;(kg)\cdot 9\cdot 10^{16}\;(m^2/s^2)=4.5\cdot 10^{20}\;(J).$ Energija reikalinga $M_0=10000\;(kg)$ masės kūnui pasiektį šviesos greitį yra $E_k={M_0 u_0^2\over 2}={M_0 c^2\over 2}=4.5\cdot 10^{20}\;(J),$ o energija reikalinga pasiekti šviesos greitį

m = 5000

kg masės kunui yra $2.25\cdot 10^{20}\;(J).$ Kai visas kuras bus išmestas (panaudotas), raketos masė pasidarys perpus mažesnė $m={M_0\over 2}=M=5000\;(kg).$ Todėl, kad kuro išmetimui pasiekti šviesos greitį reikia $2.25\cdot 10^{20}\;(J)$ energijos, o kuras turi dvigubai daugiau energijos, todėl kuro greitis yra $u_0=c\sqrt{2}$ , o raketos greitis:

$v=c\sqrt{2}\ln{M_0\over M}=\sqrt{2}\cdot 3\cdot 10^8\;(m/s)\cdot \ln{10000\;(kg)\over 5000\;(kg)}=4.242640687\cdot 10^{8}\;(m/s)\cdot 0.69314718 =$ $=294077443 \;(m/s)\approx 2.94\cdot 10^8\;(m/s) .$

Todėl, jei nepaisyti reliatyvumo teorijos, raketa pasiektų greitį 0,98c, išnaudojus visą kuro energiją anihiliacijos metu (tarkim kuro stumos naudingumas 100%), kuri sudaro pusę pradinės raketos masės.

Mastant paprastai, reikia pusė objekto masės m energijos

0.5 m c 2

, kad (tam objektui) pasiekti šviesos greitį c. O su visa objekto masės energija galima įgreitinti kuną iki greičio v, kuris randamas, taip:

${mv^2\over 2}=mc^2,$

v 2 = 2 c 2

,

$v=c\sqrt{2}=3\cdot 10^8\;(m/s)\cdot 1.414213562=424264068.7\; (m/s).$

Jeigu raketos masę sudaro 99% kuras tada kuro energija apytiksliai lygi $M_0 c^2=10000\cdot 9\cdot 10^{16}=9\cdot 10^{20}\;(J),$ o energija reikalinga pasiekti raketai šviesos greitį yra $4.5\cdot 10^{20}$ J. Todėl apytiksliai su visa kuro energija bus pasiektas greitis $c\sqrt{2}.$ Pagal formulę: