Išvestinė yra bet kokios funkcijos liestinės krypties koeficientas. Liestinė su įgaubta arba išgaubta funkcijos kreive turi tik vieną susilietimo tašką ir neturi kitų susikirtimo taškų.
Funkcijos f(x) liestinė taške x Tiesė liečia funkcijos grafiką taške
A
(
x
0
;
f
(
x
0
)
)
.
{\displaystyle A(x_{0};\;f(x_{0})).}
Kadangi tos tiesės krypties koeficientas
k
=
f
′
(
x
0
)
,
{\displaystyle k=f'(x_{0}),\;}
y
=
f
′
(
x
0
)
⋅
x
+
b
.
{\displaystyle y=f'(x_{0})\cdot x+b.}
Skaičių b sužinome iš sąlygos, kad liestinė eina per tašką A:
f
(
x
0
)
=
f
′
(
x
0
)
⋅
x
0
+
b
.
{\displaystyle f(x_{0})=f'(x_{0})\cdot x_{0}+b.}
Iš čia
b
=
f
(
x
0
)
−
f
′
(
x
0
)
⋅
x
0
.
{\displaystyle b=f(x_{0})-f'(x_{0})\cdot x_{0}.}
y
=
f
′
(
x
0
)
⋅
x
−
f
′
(
x
0
)
⋅
x
0
+
f
(
x
0
)
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
.
{\displaystyle y=f'(x_{0})\cdot x-f'(x_{0})\cdot x_{0}+f(x_{0})=f(x_{0})+f'(x_{0})(x-x_{0}).}
Tiesė liečia funkcijos
f
(
x
)
=
x
3
−
2
x
2
+
1
{\displaystyle f(x)=x^{3}-2x^{2}+1}
x
0
=
2.
{\displaystyle x_{0}=2.}
Šiame pavyzdyje
x
0
=
2
,
{\displaystyle x_{0}=2,}
f
(
x
0
)
=
f
(
2
)
=
2
3
−
2
⋅
2
2
+
1
=
1
,
{\displaystyle f(x_{0})=f(2)=2^{3}-2\cdot 2^{2}+1=1,}
f
′
(
x
)
=
3
x
2
−
4
x
,
{\displaystyle f'(x)=3x^{2}-4x,}
f
′
(
x
0
)
=
f
′
(
2
)
=
3
⋅
2
2
−
4
⋅
2
=
12
−
8
=
4.
{\displaystyle f'(x_{0})=f'(2)=3\cdot 2^{2}-4\cdot 2=12-8=4.}
y
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
=
1
+
4
(
x
−
2
)
=
4
x
−
7.
{\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0})=1+4(x-2)=4x-7.}
Tiesė liečia parabolę
y
=
x
2
{\displaystyle y=x^{2}}
x
0
{\displaystyle x_{0}}
y
(
x
0
)
=
x
0
2
,
{\displaystyle y(x_{0})=x_{0}^{2},}
y
′
(
x
0
)
=
2
x
0
.
{\displaystyle y'(x_{0})=2x_{0}.}
Įrašę tas reikšmes į liestinės lygtį, gausime:
y
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
=
x
0
2
+
2
x
0
(
x
−
x
0
)
=
2
x
0
x
−
x
0
2
.
{\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0})=x_{0}^{2}+2x_{0}(x-x_{0})=2x_{0}x-x_{0}^{2}.}
Pavyzdžiui, kai
x
0
=
1
,
{\displaystyle x_{0}=1,}
x
0
=
3
,
{\displaystyle x_{0}=3,}
y
=
2
⋅
3
x
−
3
2
=
6
x
−
9.
{\displaystyle y=2\cdot 3x-3^{2}=6x-9.}
Tiesė liečia grandininę liniją
y
=
a
cosh
(
a
x
)
=
a
2
(
e
a
x
+
e
−
a
x
)
{\displaystyle y=a\cosh(ax)={\frac {a}{2}}\left(e^{ax}+e^{-ax}\right)}
x
0
{\displaystyle x_{0}}
y
(
x
0
)
=
a
2
⋅
e
a
x
0
+
a
2
⋅
e
−
a
x
0
,
{\displaystyle y(x_{0})={\frac {a}{2}}\cdot e^{ax_{0}}+{\frac {a}{2}}\cdot e^{-ax_{0}},}
y
′
(
x
0
)
=
a
2
2
⋅
e
a
x
0
−
a
2
2
⋅
e
−
a
x
0
.
{\displaystyle y'(x_{0})={\frac {a^{2}}{2}}\cdot e^{ax_{0}}-{\frac {a^{2}}{2}}\cdot e^{-ax_{0}}.}
Įrašę tas reikšmes į liestinės lygtį, gausime:
y
l
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
=
a
2
⋅
e
a
x
0
+
a
2
⋅
e
−
a
x
0
+
(
a
2
2
⋅
e
a
x
0
−
a
2
2
⋅
e
−
a
x
0
)
(
x
−
x
0
)
.
{\displaystyle y_{l}=f(x_{0})+f'(x_{0})(x-x_{0})={\frac {a}{2}}\cdot e^{ax_{0}}+{\frac {a}{2}}\cdot e^{-ax_{0}}+({\frac {a^{2}}{2}}\cdot e^{ax_{0}}-{\frac {a^{2}}{2}}\cdot e^{-ax_{0}})(x-x_{0}).}
Pavyzdžiui, kai
x
0
=
1
,
{\displaystyle x_{0}=1,}
y
l
=
a
2
⋅
e
a
+
a
2
⋅
e
−
a
+
(
a
2
2
⋅
e
a
−
a
2
2
⋅
e
−
a
)
(
x
−
1
)
.
{\displaystyle y_{l}={\frac {a}{2}}\cdot e^{a}+{\frac {a}{2}}\cdot e^{-a}+({\frac {a^{2}}{2}}\cdot e^{a}-{\frac {a^{2}}{2}}\cdot e^{-a})(x-1).}
Pavyzdžiui, kai
x
0
=
1
,
{\displaystyle x_{0}=1,}
a
=
1
{\displaystyle a=1}
y
l
=
1
2
⋅
e
+
1
2
⋅
e
−
1
+
(
1
2
⋅
e
−
1
2
⋅
e
−
1
)
(
x
−
1
)
=
{\displaystyle y_{l}={\frac {1}{2}}\cdot e+{\frac {1}{2}}\cdot e^{-1}+({\frac {1}{2}}\cdot e-{\frac {1}{2}}\cdot e^{-1})(x-1)=}
=
1
2
⋅
e
+
1
2
⋅
e
−
1
+
(
1
2
⋅
e
−
1
2
⋅
e
−
1
)
x
−
1
2
⋅
e
+
1
2
⋅
e
−
1
=
(
1
2
⋅
e
−
1
2
⋅
e
−
1
)
x
+
e
−
1
.
{\displaystyle ={\frac {1}{2}}\cdot e+{\frac {1}{2}}\cdot e^{-1}+({\frac {1}{2}}\cdot e-{\frac {1}{2}}\cdot e^{-1})x-{\frac {1}{2}}\cdot e+{\frac {1}{2}}\cdot e^{-1}=({\frac {1}{2}}\cdot e-{\frac {1}{2}}\cdot e^{-1})x+e^{-1}.}
Kai
x
0
=
3
,
{\displaystyle x_{0}=3,}
y
l
=
a
2
⋅
e
3
a
+
a
2
⋅
e
−
3
a
+
(
a
2
2
⋅
e
3
a
−
a
2
2
⋅
e
−
3
a
)
(
x
−
3
)
.
{\displaystyle y_{l}={\frac {a}{2}}\cdot e^{3a}+{\frac {a}{2}}\cdot e^{-3a}+({\frac {a^{2}}{2}}\cdot e^{3a}-{\frac {a^{2}}{2}}\cdot e^{-3a})(x-3).}
Funkcija (žalia kreivė) ir jos liestinė taške P (mėlyna tiesė); kampas tarp liestinės taške P ir abscisės Ox yra
ϕ
,
{\displaystyle \phi ,}
tan
ϕ
=
d
y
/
d
x
.
{\displaystyle \tan \phi =dy/dx.}
Parašyti parabolės
f
(
x
)
=
x
2
{\displaystyle f(x)=x^{2}}
x
0
=
3
{\displaystyle x_{0}=3}
dy ir
Δ
y
{\displaystyle \Delta y}
x
0
=
3
{\displaystyle x_{0}=3}
Δ
x
=
1
{\displaystyle \Delta x=1}
Sprendimas . Liestinės lygtis taške
x
0
{\displaystyle x_{0}}
y
=
f
(
x
0
)
+
f
′
(
x
0
)
(
x
−
x
0
)
=
x
0
2
+
2
x
0
(
x
−
x
0
)
=
2
x
0
x
−
x
0
2
=
2
⋅
3
⋅
x
−
3
2
=
6
x
−
9.
{\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0})=x_{0}^{2}+2x_{0}(x-x_{0})=2x_{0}x-x_{0}^{2}=2\cdot 3\cdot x-3^{2}=6x-9.}
Toliau randame
Δ
y
{\displaystyle \Delta y}
Δ
y
=
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
=
(
x
0
+
Δ
x
)
2
−
x
0
2
=
x
0
2
+
2
x
0
Δ
x
+
(
Δ
x
)
2
−
x
0
2
=
{\displaystyle \Delta y=f(x_{0}+\Delta x)-f(x_{0})=(x_{0}+\Delta x)^{2}-x_{0}^{2}=x_{0}^{2}+2x_{0}\Delta x+(\Delta x)^{2}-x_{0}^{2}=}
=
2
x
0
Δ
x
+
(
Δ
x
)
2
=
2
⋅
3
⋅
1
+
1
2
=
6
+
1
=
7.
{\displaystyle =2x_{0}\Delta x+(\Delta x)^{2}=2\cdot 3\cdot 1+1^{2}=6+1=7.}
Toliau randame dy :
d
y
=
f
′
(
x
0
)
⋅
Δ
x
=
2
x
0
⋅
Δ
x
=
2
⋅
3
⋅
1
=
6.
{\displaystyle dy=f'(x_{0})\cdot \Delta x=2x_{0}\cdot \Delta x=2\cdot 3\cdot 1=6.}
Parabolės abscisės reikšmė taške
x
0
+
Δ
x
{\displaystyle x_{0}+\Delta x}
f
(
x
0
+
Δ
x
)
=
(
x
0
+
Δ
x
)
2
=
(
3
+
1
)
2
=
4
2
=
16.
{\displaystyle f(x_{0}+\Delta x)=(x_{0}+\Delta x)^{2}=(3+1)^{2}=4^{2}=16.}
Liestinės abscisės reikšmė, kai argumeno reikšmė yra
x
0
+
Δ
x
=
3
+
1
=
4
{\displaystyle x_{0}+\Delta x=3+1=4}
y
(
4
)
=
6
x
−
9
=
6
⋅
4
−
9
=
24
−
9
=
15.
{\displaystyle y(4)=6x-9=6\cdot 4-9=24-9=15.}
Na, o parabolės abscisės reikšmė nuo
x
0
+
Δ
x
=
3
+
1
=
4
{\displaystyle x_{0}+\Delta x=3+1=4}
f
(
x
0
+
Δ
x
)
=
f
(
4
)
=
(
x
0
+
Δ
x
)
2
=
4
2
=
16.
{\displaystyle f(x_{0}+\Delta x)=f(4)=(x_{0}+\Delta x)^{2}=4^{2}=16.}
Ir parabolės abscisės reikšmė taške
x
0
=
3
{\displaystyle x_{0}=3}
f
(
x
0
)
=
f
(
3
)
=
x
0
2
=
3
2
=
9.
{\displaystyle f(x_{0})=f(3)=x_{0}^{2}=3^{2}=9.}
Taigi, patikriname dy atėmę iš liestinės abscisės reikšmės nuo
x
0
+
Δ
x
=
3
+
1
=
4
{\displaystyle x_{0}+\Delta x=3+1=4}
x
0
=
3
{\displaystyle x_{0}=3}
d
y
=
y
(
x
0
+
Δ
x
)
−
f
(
x
0
)
=
y
(
4
)
−
f
(
3
)
=
15
−
9
=
6.
{\displaystyle dy=y(x_{0}+\Delta x)-f(x_{0})=y(4)-f(3)=15-9=6.}
Toliau patikriname ar tikrai
Δ
y
=
7
{\displaystyle \Delta y=7}
Δ
y
=
f
(
4
)
−
f
(
3
)
=
4
2
−
3
2
=
16
−
9
=
7.
{\displaystyle \Delta y=f(4)-f(3)=4^{2}-3^{2}=16-9=7.}
Papildomai randame
Δ
y
{\displaystyle \Delta y}
dy skirtumą:
Δ
y
−
d
y
=
7
−
6
=
1
{\displaystyle \Delta y-dy=7-6=1}
arba
Δ
y
−
d
y
=
[
2
x
0
Δ
x
+
(
Δ
x
)
2
]
−
[
(
6
(
x
0
+
Δ
x
)
−
9
)
−
x
0
2
]
=
7
−
6
=
1
,
{\displaystyle \Delta y-dy=[2x_{0}\Delta x+(\Delta x)^{2}]-[(6(x_{0}+\Delta x)-9)-x_{0}^{2}]=7-6=1,}
arba
Δ
y
−
d
y
=
[
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
]
−
[
y
(
x
0
+
Δ
x
)
−
f
(
x
0
)
]
=
7
−
6
=
1
,
{\displaystyle \Delta y-dy=[f(x_{0}+\Delta x)-f(x_{0})]-[y(x_{0}+\Delta x)-f(x_{0})]=7-6=1,}
arba
Δ
y
−
d
y
=
[
f
(
x
0
+
Δ
x
)
−
f
(
x
0
)
]
−
[
f
′
(
x
0
)
⋅
Δ
x
]
=
[
2
⋅
x
0
⋅
Δ
x
+
(
Δ
x
)
2
]
−
[
2
⋅
x
0
⋅
Δ
x
]
=
(
Δ
x
)
2
=
1
2
=
1.
{\displaystyle \Delta y-dy=[f(x_{0}+\Delta x)-f(x_{0})]-[f'(x_{0})\cdot \Delta x]=[2\cdot x_{0}\cdot \Delta x+(\Delta x)^{2}]-[2\cdot x_{0}\cdot \Delta x]=(\Delta x)^{2}=1^{2}=1.}
[ keisti ] Plokštumos, kuri liečia paviršių f(x; y) taške
A
(
x
0
;
y
0
)
{\displaystyle A(x_{0};y_{0})}
z
=
f
(
x
0
;
y
0
)
+
f
x
′
(
x
0
;
y
0
)
(
x
−
x
0
)
+
f
y
′
(
x
0
;
y
0
)
(
y
−
y
0
)
.
{\displaystyle z=f(x_{0};y_{0})+f'_{x}(x_{0};y_{0})(x-x_{0})+f'_{y}(x_{0};y_{0})(y-y_{0}).\;}
Plokštuma liečia funkcijos paviršių taške
A
(
x
0
;
y
0
;
f
(
x
0
;
y
0
)
)
.
{\displaystyle A(x_{0};\;y_{0};\;f(x_{0};\;y_{0})).}
Kadangi tos plokštumos krypties koeficientai yra
k
1
=
f
x
′
(
x
0
;
y
0
)
,
{\displaystyle k_{1}=f'_{x}(x_{0};y_{0}),\;}
k
2
=
f
y
′
(
x
0
;
y
0
)
,
{\displaystyle k_{2}=f'_{y}(x_{0};y_{0}),\;}
z
=
k
1
x
+
k
2
y
+
b
=
f
x
′
(
x
0
;
y
0
)
⋅
x
+
f
y
′
(
x
0
;
y
0
)
⋅
y
+
b
.
{\displaystyle z=k_{1}x+k_{2}y+b=f'_{x}(x_{0};y_{0})\cdot x+f'_{y}(x_{0};y_{0})\cdot y+b.}
Skaičių b sužinome iš sąlygos, kad liestinė eina per tašką A :
f
(
x
0
;
y
0
)
=
f
x
′
(
x
0
;
y
0
)
⋅
x
0
+
f
y
′
(
x
0
;
y
0
)
⋅
y
0
+
b
.
{\displaystyle f(x_{0};y_{0})=f'_{x}(x_{0};y_{0})\cdot x_{0}+f'_{y}(x_{0};y_{0})\cdot y_{0}+b.}
Iš čia
b
=
f
(
x
0
;
y
0
)
−
f
x
′
(
x
0
;
y
0
)
⋅
x
0
−
f
y
′
(
x
0
;
y
0
)
⋅
y
0
.
{\displaystyle b=f(x_{0};y_{0})-f'_{x}(x_{0};y_{0})\cdot x_{0}-f'_{y}(x_{0};y_{0})\cdot y_{0}.}
z
=
k
1
x
+
k
2
y
+
b
=
f
x
′
(
x
0
;
y
0
)
⋅
x
+
f
y
′
(
x
0
;
y
0
)
⋅
y
+
f
(
x
0
;
y
0
)
−
f
x
′
(
x
0
;
y
0
)
⋅
x
0
−
f
y
′
(
x
0
;
y
0
)
⋅
y
0
=
{\displaystyle z=k_{1}x+k_{2}y+b=f'_{x}(x_{0};y_{0})\cdot x+f'_{y}(x_{0};y_{0})\cdot y+f(x_{0};y_{0})-f'_{x}(x_{0};y_{0})\cdot x_{0}-f'_{y}(x_{0};y_{0})\cdot y_{0}=}
=
(
x
−
x
0
)
⋅
f
x
′
(
x
0
;
y
0
)
+
(
y
−
y
0
)
⋅
f
y
′
(
x
0
;
y
0
)
+
f
(
x
0
;
y
0
)
=
(
x
−
x
0
)
⋅
f
x
′
(
x
0
;
y
0
)
+
(
y
−
y
0
)
⋅
f
y
′
(
x
0
;
y
0
)
+
z
0
.
{\displaystyle =(x-x_{0})\cdot f'_{x}(x_{0};y_{0})+(y-y_{0})\cdot f'_{y}(x_{0};y_{0})+f(x_{0};y_{0})=(x-x_{0})\cdot f'_{x}(x_{0};y_{0})+(y-y_{0})\cdot f'_{y}(x_{0};y_{0})+z_{0}.}
Pavyzdys . Rasti liečiamosios plokštumos lygtį taške A (3; 4; 27) funkcijos, kuri nusako paviršių
f
(
x
;
y
)
=
100
−
x
2
−
y
3
.
{\displaystyle f(x;y)=100-x^{2}-y^{3}.}
Sprendimas .
f
(
3
;
4
)
=
100
−
3
2
−
4
3
=
100
−
9
−
64
=
27.
{\displaystyle f(3;4)=100-3^{2}-4^{3}=100-9-64=27.}
f
x
′
(
x
0
;
y
0
)
=
−
2
x
.
{\displaystyle f'_{x}(x_{0};y_{0})=-2x.\;}
f
y
′
(
x
0
;
y
0
)
=
−
3
y
2
.
{\displaystyle f'_{y}(x_{0};y_{0})=-3y^{2}.\;}
f
x
′
(
3
;
4
)
=
−
2
⋅
3
=
−
6.
{\displaystyle f'_{x}(3;4)=-2\cdot 3=-6.}
f
y
′
(
3
;
4
)
=
−
3
⋅
4
2
=
−
48.
{\displaystyle f'_{y}(3;4)=-3\cdot 4^{2}=-48.}
Liečiamosios plokštumos lygtis yra:
z
=
(
x
−
x
0
)
⋅
f
x
′
(
x
0
;
y
0
)
+
(
y
−
y
0
)
⋅
f
y
′
(
x
0
;
y
0
)
+
z
0
=
(
x
−
3
)
⋅
(
−
6
)
+
(
y
−
4
)
⋅
(
−
48
)
+
27
=
−
6
x
+
18
−
48
y
+
192
+
27
=
−
6
x
−
48
y
+
237.
{\displaystyle z=(x-x_{0})\cdot f'_{x}(x_{0};y_{0})+(y-y_{0})\cdot f'_{y}(x_{0};y_{0})+z_{0}=(x-3)\cdot (-6)+(y-4)\cdot (-48)+27=-6x+18-48y+192+27=-6x-48y+237.}
Pavyzdys . Rasti liečiamosios plokštumos lygtį taške A (8; 4; 172) funkcijos, kuri nusako paviršių
f
(
x
;
y
)
=
300
−
x
2
−
y
3
.
{\displaystyle f(x;y)=300-x^{2}-y^{3}.}
Sprendimas .
f
(
3
;
4
)
=
300
−
8
2
−
4
3
=
300
−
64
−
64
=
172.
{\displaystyle f(3;4)=300-8^{2}-4^{3}=300-64-64=172.}
f
x
′
(
x
0
;
y
0
)
=
−
2
x
.
{\displaystyle f'_{x}(x_{0};y_{0})=-2x.\;}
f
y
′
(
x
0
;
y
0
)
=
−
3
y
2
.
{\displaystyle f'_{y}(x_{0};y_{0})=-3y^{2}.\;}
f
x
′
(
3
;
4
)
=
−
2
⋅
8
=
−
16.
{\displaystyle f'_{x}(3;4)=-2\cdot 8=-16.}
f
y
′
(
3
;
4
)
=
−
3
⋅
4
2
=
−
48.
{\displaystyle f'_{y}(3;4)=-3\cdot 4^{2}=-48.}
Liečiamosios plokštumos lygtis yra:
z
=
(
x
−
x
0
)
⋅
f
x
′
(
x
0
;
y
0
)
+
(
y
−
y
0
)
⋅
f
y
′
(
x
0
;
y
0
)
+
z
0
=
(
x
−
8
)
⋅
(
−
16
)
+
(
y
−
4
)
⋅
(
−
48
)
+
172
=
{\displaystyle z=(x-x_{0})\cdot f'_{x}(x_{0};y_{0})+(y-y_{0})\cdot f'_{y}(x_{0};y_{0})+z_{0}=(x-8)\cdot (-16)+(y-4)\cdot (-48)+172=}
=
−
16
x
+
144
−
48
y
+
192
+
172
=
−
16
x
−
48
y
+
508.
{\displaystyle =-16x+144-48y+192+172=-16x-48y+508.}
Pavyzdys . Rasti liečiamosios plokštumos lygtį taške A (8; 4; 0) funkcijos, kuri nusako paviršių
f
(
x
;
y
)
=
128
−
x
2
−
y
3
.
{\displaystyle f(x;y)=128-x^{2}-y^{3}.}
Sprendimas .
f
(
3
;
4
)
=
128
−
8
2
−
4
3
=
128
−
64
−
64
=
0.
{\displaystyle f(3;4)=128-8^{2}-4^{3}=128-64-64=0.}
f
x
′
(
x
0
;
y
0
)
=
−
2
x
.
{\displaystyle f'_{x}(x_{0};y_{0})=-2x.\;}
f
y
′
(
x
0
;
y
0
)
=
−
3
y
2
.
{\displaystyle f'_{y}(x_{0};y_{0})=-3y^{2}.\;}
f
x
′
(
3
;
4
)
=
−
2
⋅
8
=
−
16.
{\displaystyle f'_{x}(3;4)=-2\cdot 8=-16.}
f
y
′
(
3
;
4
)
=
−
3
⋅
4
2
=
−
48.
{\displaystyle f'_{y}(3;4)=-3\cdot 4^{2}=-48.}
Liečiamosios plokštumos lygtis yra:
z
=
(
x
−
x
0
)
⋅
f
x
′
(
x
0
;
y
0
)
+
(
y
−
y
0
)
⋅
f
y
′
(
x
0
;
y
0
)
+
z
0
=
(
x
−
8
)
⋅
(
−
16
)
+
(
y
−
4
)
⋅
(
−
48
)
+
0
=
−
16
x
+
144
−
48
y
+
192
=
−
16
x
−
48
y
+
336.
{\displaystyle z=(x-x_{0})\cdot f'_{x}(x_{0};y_{0})+(y-y_{0})\cdot f'_{y}(x_{0};y_{0})+z_{0}=(x-8)\cdot (-16)+(y-4)\cdot (-48)+0=-16x+144-48y+192=-16x-48y+336.}
[ keisti ] Žinome, kad plokštuma
A
(
x
−
x
0
)
+
B
(
y
−
y
0
)
+
C
(
z
−
z
0
)
=
0
;
{\displaystyle A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0;}
A
x
+
B
y
+
C
z
+
(
−
A
x
0
−
B
y
0
−
C
z
0
)
=
0
;
{\displaystyle Ax+By+Cz+(-Ax_{0}-By_{0}-Cz_{0})=0;}
A
x
+
B
y
+
C
z
+
D
=
0
,
D
=
−
A
x
0
−
B
y
0
−
C
z
0
{\displaystyle Ax+By+Cz+D=0,\;\;D=-Ax_{0}-By_{0}-Cz_{0}}
turi normalės vektorių
n
→
=
(
A
;
B
;
C
)
{\displaystyle {\vec {n}}=(A;B;C)}
A
x
+
B
y
+
C
z
+
D
=
0
{\displaystyle Ax+By+Cz+D=0}
A
x
+
B
y
+
C
z
+
D
=
0
{\displaystyle Ax+By+Cz+D=0}
A
(
x
0
;
y
0
;
z
0
)
{\displaystyle A(x_{0};\;y_{0};\;z_{0})}
x
−
x
0
A
=
y
−
y
0
B
=
z
−
z
0
C
.
{\displaystyle {\frac {x-x_{0}}{A}}={\frac {y-y_{0}}{B}}={\frac {z-z_{0}}{C}}.}
Analogiškai, perrašius paviršių liečiančią plokštumą
z
=
f
(
x
0
;
y
0
)
+
f
x
′
(
x
0
;
y
0
)
(
x
−
x
0
)
+
f
y
′
(
x
0
;
y
0
)
(
y
−
y
0
)
,
{\displaystyle z=f(x_{0};y_{0})+f'_{x}(x_{0};y_{0})(x-x_{0})+f'_{y}(x_{0};y_{0})(y-y_{0}),\;}
z
−
z
0
=
f
x
′
(
x
0
;
y
0
)
(
x
−
x
0
)
+
f
y
′
(
x
0
;
y
0
)
(
y
−
y
0
)
,
{\displaystyle z-z_{0}=f'_{x}(x_{0};y_{0})(x-x_{0})+f'_{y}(x_{0};y_{0})(y-y_{0}),\;}
0
=
f
x
′
(
x
0
;
y
0
)
(
x
−
x
0
)
+
f
y
′
(
x
0
;
y
0
)
(
y
−
y
0
)
−
(
z
−
z
0
)
,
{\displaystyle 0=f'_{x}(x_{0};y_{0})(x-x_{0})+f'_{y}(x_{0};y_{0})(y-y_{0})-(z-z_{0}),\;}
f
x
′
(
x
0
;
y
0
)
(
x
−
x
0
)
+
f
y
′
(
x
0
;
y
0
)
(
y
−
y
0
)
−
(
z
−
z
0
)
=
0
,
{\displaystyle f'_{x}(x_{0};y_{0})(x-x_{0})+f'_{y}(x_{0};y_{0})(y-y_{0})-(z-z_{0})=0,\;}
gauname paviršių liečiančios plokštumos normalės lygtį taške
A
(
x
0
;
y
0
;
z
0
)
:
{\displaystyle A(x_{0};y_{0};z_{0}):}
x
−
x
0
f
x
′
(
x
0
;
y
0
)
=
y
−
y
0
f
y
′
(
x
0
;
y
0
)
=
z
−
z
0
−
1
.
{\displaystyle {\frac {x-x_{0}}{f'_{x}(x_{0};y_{0})}}={\frac {y-y_{0}}{f'_{y}(x_{0};y_{0})}}={\frac {z-z_{0}}{-1}}.}
Vadinasi paviršių liečiančios plokštumos normalės vektorius yra
n
→
=
(
f
x
′
(
x
0
;
y
0
)
;
f
y
′
(
x
0
;
y
0
)
;
−
1
)
.
{\displaystyle {\vec {n}}=(f'_{x}(x_{0};y_{0});\;f'_{y}(x_{0};y_{0});\;-1).}
Bendri atvejai:
d
d
x
C
=
0
{\displaystyle {\frac {\,d}{\,dx}}\,C=0}
d
d
x
x
n
=
n
x
n
−
1
{\displaystyle {\frac {\,d}{\,dx}}x^{n}=nx^{n-1}}
Logaritminės funkcijos:
d
d
x
ln
x
=
1
x
{\displaystyle {\frac {\,d}{\,dx}}\ln x={\frac {1}{x}}}
log
b
x
=
1
x
ln
b
{\displaystyle \log _{b}x={\frac {1}{x\ln b}}}
Rodiklinės funkcijos:
d
d
x
e
x
=
e
x
ln
e
=
e
x
{\displaystyle {\frac {\,d}{\,dx}}e^{x}=e^{x}\ln e=e^{x}}
d
d
x
a
x
=
a
x
log
e
a
=
a
x
ln
a
{\displaystyle {\frac {d}{\,dx}}a^{x}=a^{x}\log _{e}a=a^{x}\ln a}
Trigonometrinės funkcijos
d
d
x
sin
x
=
cos
x
{\displaystyle {\frac {\,d}{\,dx}}\sin x=\cos x}
d
d
x
cos
x
=
−
sin
x
{\displaystyle {\frac {\,d}{\,dx}}\cos x=-\sin x}
d
d
x
tan
x
=
sec
2
x
=
1
cos
2
x
{\displaystyle {d \over dx}\tan x=\sec ^{2}x={1 \over \cos ^{2}x}}
d
d
x
csc
x
=
(
1
sin
x
)
′
=
−
csc
x
cot
x
=
−
cos
x
sin
2
x
{\displaystyle {\frac {\,d}{\,dx}}\csc x=({\frac {1}{\sin x}})'=-\csc x\cot x=-{\frac {\cos x}{\sin ^{2}x}}}
d
d
x
sec
x
=
(
1
cos
x
)
′
=
sin
x
cos
2
x
=
sec
x
tan
x
{\displaystyle {\frac {\,d}{\,dx}}\sec x=({\frac {1}{\cos x}})'={\frac {\sin x}{\cos ^{2}x}}=\sec x\tan x}
d
d
x
cot
x
=
−
csc
2
x
=
−
1
sin
2
x
{\displaystyle {d \over dx}\cot x=-\csc ^{2}x={-1 \over \sin ^{2}x}}
[ keisti ] Bendri atvejai:
(
x
m
)
(
n
)
=
m
(
m
−
1
)
(
m
−
2
)
(
m
−
3
)
.
.
.
(
m
−
n
+
1
)
x
m
−
n
{\displaystyle (x^{m})^{(n)}=m(m-1)(m-2)(m-3)...(m-n+1)x^{m-n}}
(
a
x
)
(
n
)
=
a
x
ln
n
a
{\displaystyle (a^{x})^{(n)}=a^{x}\ln ^{n}a}
(
e
x
)
(
n
)
=
e
x
{\displaystyle (e^{x})^{(n)}=e^{x}}
Tiesinės trupmeninės funkcijos n-toji išvestinė:
(
a
x
+
b
c
x
+
d
)
(
n
)
=
(
a
d
−
b
c
)
(
−
1
)
n
−
1
n
!
(
c
x
+
d
)
−
n
−
1
c
n
−
1
{\displaystyle ({\frac {ax+b}{cx+d}})^{(n)}=(ad-bc)(-1)^{n-1}n!(cx+d)^{-n-1}c^{n-1}}
Sandaugos išvestinė sutampa su binomo formule , tik vietoje laipsnio rašoma išvestinė:
(
u
v
)
(
n
)
=
u
(
n
)
v
+
C
n
1
u
(
n
−
1
)
v
′
+
C
n
2
u
(
n
−
2
)
v
(
2
)
+
C
n
3
u
(
n
−
3
)
v
(
3
)
+
⋯
+
u
v
(
n
)
{\displaystyle (uv)^{(n)}=u^{(n)}v+C_{n}^{1}u^{(n-1)}v'+C_{n}^{2}u^{(n-2)}v^{(2)}+C_{n}^{3}u^{(n-3)}v^{(3)}+\dots +uv^{(n)}}
Trigonometrijoje:
(
sin
x
)
(
n
)
=
sin
(
x
+
n
π
2
)
{\displaystyle (\sin x)^{(n)}=\sin(x+n{\frac {\pi }{2}})}
(
cos
x
)
(
n
)
=
cos
(
x
+
n
π
2
)
{\displaystyle (\cos x)^{(n)}=\cos(x+n{\frac {\pi }{2}})}
kur (n) yra n-tos eilės išvestinė.
Sinuso išvestinės įrodymas . Funkcija
y
=
sin
x
{\displaystyle y=\sin x}
y
′
=
cos
x
{\displaystyle y'=\cos x}
sin
A
±
sin
B
=
2
⋅
sin
(
A
±
B
2
)
⋅
cos
(
A
∓
B
2
)
,
{\displaystyle \sin A\pm \sin B=2\cdot \sin({\frac {A\pm B}{2}})\cdot \cos({\frac {A\mp B}{2}}),}
sin
A
−
sin
B
=
2
⋅
sin
(
A
−
B
2
)
⋅
cos
(
A
+
B
2
)
.
{\displaystyle \sin A-\sin B=2\cdot \sin({\frac {A-B}{2}})\cdot \cos({\frac {A+B}{2}}).}
x priaugimą
Δ
x
{\displaystyle \Delta x}
1)
y
+
Δ
y
=
sin
(
x
+
Δ
x
)
{\displaystyle y+\Delta y=\sin(x+\Delta x)}
2)
Δ
y
=
sin
(
x
+
Δ
x
)
−
sin
x
=
2
⋅
sin
(
x
+
Δ
x
−
x
2
)
⋅
cos
(
x
+
Δ
x
+
x
2
)
=
2
⋅
sin
Δ
x
2
⋅
cos
(
x
+
Δ
x
2
)
;
{\displaystyle \Delta y=\sin(x+\Delta x)-\sin x=2\cdot \sin({\frac {x+\Delta x-x}{2}})\cdot \cos({\frac {x+\Delta x+x}{2}})=2\cdot \sin {\frac {\Delta x}{2}}\cdot \cos(x+{\frac {\Delta x}{2}});}
3)
Δ
y
Δ
x
=
2
⋅
sin
Δ
x
2
⋅
cos
(
x
+
Δ
x
2
)
Δ
x
=
sin
Δ
x
2
Δ
x
2
cos
(
x
+
Δ
x
2
)
;
{\displaystyle {\frac {\Delta y}{\Delta x}}={\frac {2\cdot \sin {\frac {\Delta x}{2}}\cdot \cos(x+{\frac {\Delta x}{2}})}{\Delta x}}={\frac {\sin {\Delta x \over 2}}{\Delta x \over 2}}\cos \left(x+{\frac {\Delta x}{2}}\right);}
4)
y
′
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
lim
Δ
x
→
0
sin
Δ
x
2
Δ
x
2
cos
(
x
+
Δ
x
2
)
;
{\displaystyle y'=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {\sin {\Delta x \over 2}}{\Delta x \over 2}}\cos \left(x+{\frac {\Delta x}{2}}\right);}
Žinome, kad
lim
Δ
x
→
0
sin
(
Δ
x
)
Δ
x
=
1
,
{\displaystyle \lim _{\Delta x\to 0}{\frac {\sin(\Delta x)}{\Delta x}}=1,}
lim
Δ
x
→
0
sin
Δ
x
2
Δ
x
2
=
1
,
{\displaystyle \lim _{\Delta x\to 0}{\frac {\sin {\Delta x \over 2}}{\Delta x \over 2}}=1,}
tai
y
′
=
lim
Δ
x
→
0
cos
(
x
+
Δ
x
2
)
=
cos
x
.
{\displaystyle y'=\lim _{\Delta x\to 0}\cos \left(x+{\frac {\Delta x}{2}}\right)=\cos x.}
Kosinuso išvestinės įrodymas . Išvestinė funkcijos
y
=
cos
x
{\displaystyle y=\cos x}
y
′
=
−
sin
x
.
{\displaystyle y'=-\sin x.\;}
Įrodymas . Pasinaudodami formule
cos
A
−
cos
B
=
−
2
⋅
sin
(
A
+
B
2
)
⋅
sin
(
A
−
B
2
)
,
{\displaystyle \cos A-\cos B=-2\cdot \sin \left({\frac {A+B}{2}}\right)\cdot \sin \left({\frac {A-B}{2}}\right),}
Δ
y
=
cos
(
x
+
Δ
x
)
−
cos
x
=
−
2
⋅
sin
(
(
x
+
Δ
x
)
+
x
2
)
⋅
sin
(
(
x
+
Δ
x
)
−
x
2
)
=
−
2
⋅
sin
(
x
+
Δ
x
2
)
⋅
sin
(
Δ
x
2
)
.
{\displaystyle \Delta y=\cos(x+\Delta x)-\cos x=-2\cdot \sin \left({\frac {(x+\Delta x)+x}{2}}\right)\cdot \sin \left({\frac {(x+\Delta x)-x}{2}}\right)=-2\cdot \sin \left(x+{\frac {\Delta x}{2}}\right)\cdot \sin \left({\frac {\Delta x}{2}}\right).}
Tokiu budu, kai
Δ
x
≠
0
,
{\displaystyle \Delta x\neq 0,}
Δ
y
Δ
x
=
−
2
⋅
sin
(
x
+
Δ
x
2
)
⋅
sin
(
Δ
x
2
)
Δ
x
=
−
sin
(
x
+
Δ
x
2
)
⋅
sin
(
Δ
x
2
)
Δ
x
2
.
{\displaystyle {\frac {\Delta y}{\Delta x}}=-{\frac {2\cdot \sin \left(x+{\frac {\Delta x}{2}}\right)\cdot \sin \left({\frac {\Delta x}{2}}\right)}{\Delta x}}=-\sin \left(x+{\frac {\Delta x}{2}}\right)\cdot {\frac {\sin \left({\frac {\Delta x}{2}}\right)}{\frac {\Delta x}{2}}}.}
Turime, kad
lim
Δ
x
→
0
sin
Δ
x
2
Δ
x
2
=
1
{\displaystyle \lim _{\Delta x\to 0}{\frac {\sin {\Delta x \over 2}}{\Delta x \over 2}}=1}
y
′
=
(
cos
x
)
′
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
lim
Δ
x
→
0
(
−
sin
(
x
+
Δ
x
2
)
⋅
sin
(
Δ
x
2
)
Δ
x
2
)
=
lim
Δ
x
→
0
(
−
sin
(
x
+
Δ
x
2
)
⋅
1
)
=
−
sin
x
.
{\displaystyle y'=(\cos x)'=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=\lim _{\Delta x\to 0}\left(-\sin \left(x+{\frac {\Delta x}{2}}\right)\cdot {\frac {\sin \left({\frac {\Delta x}{2}}\right)}{\frac {\Delta x}{2}}}\right)=\lim _{\Delta x\to 0}\left(-\sin \left(x+{\frac {\Delta x}{2}}\right)\cdot 1\right)=-\sin x.}
Įrodymas išvestinės funkcijos
y
=
log
a
x
(
0
<
a
≠
1
)
{\displaystyle y=\log _{a}x\;(0<a\neq 1)}
y
′
=
1
x
log
a
e
=
1
x
ln
a
,
{\displaystyle y'={\frac {1}{x}}\log _{a}{\text{e}}={\frac {1}{x\ln a}},}
kadangi žinoma iš elementarios matematikos, kad
log
a
b
=
1
log
b
a
.
{\displaystyle \log _{a}b={\frac {1}{\log _{b}a}}.}
log
a
b
−
log
a
c
=
log
a
b
c
,
{\displaystyle \log _{a}b-\log _{a}c=\log _{a}{\frac {b}{c}},}
Δ
y
=
log
a
(
x
+
Δ
x
)
−
log
a
x
=
log
a
x
+
Δ
x
x
=
log
a
(
1
+
Δ
x
x
)
.
{\displaystyle \Delta y=\log _{a}(x+\Delta x)-\log _{a}x=\log _{a}{\frac {x+\Delta x}{x}}=\log _{a}\left(1+{\frac {\Delta x}{x}}\right).}
Tokiu budu, kai
Δ
x
≠
0
,
{\displaystyle \Delta x\neq 0,}
Δ
y
Δ
x
=
1
Δ
x
log
a
(
1
+
Δ
x
x
)
=
1
x
⋅
x
Δ
x
⋅
log
a
(
1
+
Δ
x
x
)
=
1
x
log
a
[
(
1
+
Δ
x
x
)
x
Δ
x
]
.
{\displaystyle {\frac {\Delta y}{\Delta x}}={\frac {1}{\Delta x}}\log _{a}\left(1+{\frac {\Delta x}{x}}\right)={\frac {1}{x}}\cdot {\frac {x}{\Delta x}}\cdot \log _{a}\left(1+{\frac {\Delta x}{x}}\right)={\frac {1}{x}}\log _{a}\left[\left(1+{\frac {\Delta x}{x}}\right)^{\frac {x}{\Delta x}}\right].}
Pakeitę
x
Δ
x
=
h
,
{\displaystyle {\frac {x}{\Delta x}}=h,}
lim
Δ
x
→
0
(
1
+
Δ
x
x
)
x
Δ
x
=
lim
h
→
∞
(
1
+
1
h
)
h
=
e
.
{\displaystyle \lim _{\Delta x\rightarrow 0}\left(1+{\frac {\Delta x}{x}}\right)^{\frac {x}{\Delta x}}=\lim _{h\to \infty }\left(1+{\frac {1}{h}}\right)^{h}={\text{e}}.}
O kadangi logaritminė funkcija yra netruki, tai
y
′
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
1
x
log
a
[
(
1
+
Δ
x
x
)
x
Δ
x
]
=
1
x
log
a
e
=
1
x
ln
a
.
{\displaystyle y'=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}={\frac {1}{x}}\log _{a}\left[\left(1+{\frac {\Delta x}{x}}\right)^{\frac {x}{\Delta x}}\right]={\frac {1}{x}}\log _{a}{\text{e}}={\frac {1}{x\ln a}}.}
Iš to seka, kad jeigu
y
=
log
e
x
=
ln
x
,
{\displaystyle y=\log _{e}x=\ln x,}
y
′
=
(
ln
x
)
′
=
1
x
ln
e
=
1
x
.
{\displaystyle y'=(\ln x)'={\frac {1}{x\ln {\text{e}}}}={\frac {1}{x}}.}
Tangento išvestinės įrodymas . Įrodysime, kad
y
′
=
(
tan
x
)
′
=
1
cos
2
x
=
sec
2
x
.
{\displaystyle y'=(\tan x)'={\frac {1}{\cos ^{2}x}}=\sec ^{2}x.}
Įrodymas .
y
′
=
(
tan
x
)
′
=
(
sin
x
cos
x
)
′
=
(
sin
x
)
′
cos
x
−
sin
x
(
cos
x
)
′
cos
2
x
=
cos
x
cos
x
−
sin
x
(
−
sin
x
)
cos
2
x
=
.
{\displaystyle y'=(\tan x)'=({\frac {\sin x}{\cos x}})'={\frac {(\sin x)'\cos x-\sin x(\cos x)'}{\cos ^{2}x}}={\frac {\cos x\cos x-\sin x(-\sin x)}{\cos ^{2}x}}=.}
=
cos
2
x
+
sin
2
x
cos
2
x
=
1
cos
2
x
=
1
+
tan
2
x
=
sec
2
x
.
{\displaystyle ={\frac {\cos ^{2}x+\sin ^{2}x}{\cos ^{2}x}}={\frac {1}{\cos ^{2}x}}=1+\tan ^{2}x=\sec ^{2}x.}
Arktangento išvestinės įrodymas . Įrodysime, kad
y
′
=
(
arctan
x
)
′
=
1
1
+
x
2
.
{\displaystyle y'=(\arctan x)'={\frac {1}{1+x^{2}}}.}
Įrodymas .
y
=
arctan
x
,
{\displaystyle y=\arctan x,}
tan
y
=
tan
(
arctan
x
)
,
{\displaystyle \tan y=\tan(\arctan x),}
tan
y
=
x
,
{\displaystyle \tan y=x,}
d
d
x
(
tan
y
)
=
d
d
x
(
x
)
,
{\displaystyle {\frac {d}{dx}}(\tan y)={\frac {d}{dx}}(x),}
1
cos
2
y
d
y
d
x
=
1
,
{\displaystyle {\frac {1}{\cos ^{2}y}}{\frac {dy}{dx}}=1,}
sec
2
(
y
)
d
y
d
x
=
1
,
{\displaystyle \sec ^{2}(y){\frac {dy}{dx}}=1,}
d
y
d
x
=
1
sec
2
y
,
{\displaystyle {\frac {dy}{dx}}={\frac {1}{\sec ^{2}y}},}
d
y
d
x
=
1
1
+
tan
2
y
;
{\displaystyle {\frac {dy}{dx}}={\frac {1}{1+\tan ^{2}y}};}
iš trečios eilutės turime, kad
tan
y
=
x
,
{\displaystyle \tan y=x,}
d
y
d
x
=
1
1
+
x
2
.
{\displaystyle {\frac {dy}{dx}}={\frac {1}{1+x^{2}}}.}
Arksinuso išvestinės įrodymas . Įrodysime, kad funkcijos
y
=
arcsin
x
{\displaystyle y=\arcsin x}
y
′
=
(
arcsin
x
)
′
=
1
1
−
x
2
.
{\displaystyle y'=(\arcsin x)'={\frac {1}{\sqrt {1-x^{2}}}}.}
Įrodymas .
y
=
arcsin
x
,
{\displaystyle y=\arcsin x,}
sin
y
=
sin
(
arcsin
x
)
,
{\displaystyle \sin y=\sin(\arcsin x),}
sin
y
=
x
,
{\displaystyle \sin y=x,}
d
d
x
(
sin
y
)
=
d
d
x
(
x
)
,
{\displaystyle {\frac {d}{dx}}(\sin y)={\frac {d}{dx}}(x),}
cos
(
y
)
d
y
d
x
=
1
,
{\displaystyle \cos(y){\frac {dy}{dx}}=1,}
d
y
d
x
=
1
cos
y
,
{\displaystyle {\frac {dy}{dx}}={\frac {1}{\cos y}},}
d
y
d
x
=
1
1
−
sin
2
y
;
{\displaystyle {\frac {dy}{dx}}={\frac {1}{\sqrt {1-\sin ^{2}y}}};}
iš trečios eilutės turime, kad
sin
y
=
x
,
{\displaystyle \sin y=x,}
d
y
d
x
=
1
1
−
x
2
.
{\displaystyle {\frac {dy}{dx}}={\frac {1}{\sqrt {1-x^{2}}}}.}
Arkkosinuso išvestinės įrodymas . Įrodysime, kad funkcijos
y
=
arccos
x
{\displaystyle y=\arccos x}
y
′
=
(
arccos
x
)
′
=
−
1
1
−
x
2
.
{\displaystyle y'=(\arccos x)'={\frac {-1}{\sqrt {1-x^{2}}}}.}
Įrodymas .
y
=
arccos
x
,
{\displaystyle y=\arccos x,}
cos
y
=
cos
(
arccos
x
)
,
{\displaystyle \cos y=\cos(\arccos x),}
cos
y
=
x
,
{\displaystyle \cos y=x,}
d
d
x
(
cos
y
)
=
d
d
x
(
x
)
,
{\displaystyle {\frac {d}{dx}}(\cos y)={\frac {d}{dx}}(x),}
−
sin
(
y
)
d
y
d
x
=
1
,
{\displaystyle -\sin(y){\frac {dy}{dx}}=1,}
d
y
d
x
=
−
1
sin
y
,
{\displaystyle {\frac {dy}{dx}}={\frac {-1}{\sin y}},}
d
y
d
x
=
−
1
1
−
cos
2
y
;
{\displaystyle {\frac {dy}{dx}}={\frac {-1}{\sqrt {1-\cos ^{2}y}}};}
iš trečios eilutės turime, kad
cos
y
=
x
,
{\displaystyle \cos y=x,}
d
y
d
x
=
−
1
1
−
x
2
.
{\displaystyle {\frac {dy}{dx}}={\frac {-1}{\sqrt {1-x^{2}}}}.}
Išvestinė rodiklinės funkcijos . Išvestinė funkcijos
y
=
a
x
(
0
<
a
≠
1
)
{\displaystyle y=a^{x}\;\;(0<a\neq 1)}
y
′
=
a
x
ln
a
.
{\displaystyle y'=a^{x}\ln a.}
Įrodymas .
y
=
a
x
,
{\displaystyle y=a^{x},}
ln
y
=
ln
a
x
,
{\displaystyle \ln y=\ln a^{x},}
ln
y
=
x
ln
a
,
{\displaystyle \ln y=x\ln a,}
d
d
x
(
ln
y
)
=
ln
(
a
)
d
d
x
(
x
)
,
{\displaystyle {\frac {d}{dx}}(\ln y)=\ln(a){\frac {d}{dx}}(x),}
d
d
y
(
ln
y
)
d
y
d
x
=
ln
(
a
)
⋅
1
,
{\displaystyle {\frac {d}{dy}}(\ln y){\frac {dy}{dx}}=\ln(a)\cdot 1,}
1
y
d
y
d
x
=
ln
(
a
)
,
{\displaystyle {\frac {1}{y}}{\frac {dy}{dx}}=\ln(a),}
d
y
d
x
=
y
ln
(
a
)
,
{\displaystyle {\frac {dy}{dx}}=y\ln(a),}
bet
y
=
a
x
,
{\displaystyle y=a^{x},}
d
y
d
x
=
a
x
ln
a
.
{\displaystyle {\frac {dy}{dx}}=a^{x}\ln a.}
[ keisti ]
x
y
′
=
1
y
x
′
,
{\displaystyle x_{y}'={\frac {1}{y_{x}'}},}
Δ
x
Δ
y
=
1
Δ
y
Δ
x
.
{\displaystyle {\frac {\Delta x}{\Delta y}}={\frac {1}{\frac {\Delta y}{\Delta x}}}.}
Todėl
y
x
′
=
1
x
y
′
.
{\displaystyle y_{x}'={\frac {1}{x_{y}'}}.}
Rasime išvestinę funkcijos
y
=
arcsin
x
,
{\displaystyle y=\arcsin x,}
|
x
|
<
1
{\displaystyle |x|<1}
|
y
|
<
π
2
.
{\displaystyle |y|<{\frac {\pi }{2}}.}
x
=
sin
y
{\displaystyle x=\sin y}
−
π
2
<
y
<
π
2
;
{\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}};}
x
y
′
=
cos
y
.
{\displaystyle x_{y}'=\cos y.}
(
arcsin
x
)
′
=
1
(
sin
y
)
′
=
1
cos
y
=
1
1
−
sin
2
y
=
1
1
−
(
sin
(
arcsin
x
)
)
2
=
1
1
−
x
2
,
{\displaystyle (\arcsin x)'={\frac {1}{(\sin y)'}}={\frac {1}{\cos y}}={\frac {1}{\sqrt {1-\sin ^{2}y}}}={\frac {1}{\sqrt {1-(\sin(\arcsin x))^{2}}}}={\frac {1}{\sqrt {1-x^{2}}}},}
nes
cos
y
>
0
,
{\displaystyle \cos y>0,}
|
y
|
<
π
2
.
{\displaystyle |y|<{\frac {\pi }{2}}.}
y
=
arctan
x
,
{\displaystyle y=\arctan x,}
x
=
tan
y
{\displaystyle x=\tan y}
x
y
′
=
(
tan
y
)
′
=
1
cos
2
y
.
{\displaystyle x_{y}'=(\tan y)'={\frac {1}{\cos ^{2}y}}.}
(
arctan
x
)
′
=
1
(
tan
y
)
′
=
1
1
cos
2
y
=
1
1
+
tan
2
y
=
1
1
+
tan
2
(
arctan
x
)
=
1
1
+
x
2
,
{\displaystyle (\arctan x)'={\frac {1}{(\tan y)'}}={\frac {1}{\frac {1}{\cos ^{2}y}}}={\frac {1}{1+\tan ^{2}y}}={\frac {1}{1+\tan ^{2}(\arctan x)}}={\frac {1}{1+x^{2}}},}
kur
1
+
tan
2
A
=
1
cos
2
A
{\displaystyle 1+\tan ^{2}A={\frac {1}{\cos ^{2}A}}}
Išvestinė rodiklinės funkcijos . Išvestinė funkcijos
y
=
a
x
(
0
<
a
≠
1
)
{\displaystyle y=a^{x}\;\;(0<a\neq 1)}
y
′
=
a
x
ln
a
.
{\displaystyle y'=a^{x}\ln a.}
Įrodymas . Rodiklinė funkcija
y
=
a
x
{\displaystyle y=a^{x}}
x
=
log
a
y
.
{\displaystyle x=\log _{a}y.}
x
′
(
y
)
=
1
y
log
a
e
,
{\displaystyle x'(y)={\frac {1}{y}}\log _{a}e,}
tai pagal teoremą apie išvestinę atvirkštinės funkcijos ir žinomo iš elementariosios matematikos santykio
log
a
b
=
1
log
b
a
{\displaystyle \log _{a}b={\frac {1}{\log _{b}a}}}
y
′
(
x
)
=
1
x
′
(
y
)
=
y
log
a
e
=
y
log
e
a
=
a
x
ln
a
.
{\displaystyle y'(x)={\frac {1}{x'(y)}}={\frac {y}{\log _{a}e}}=y\log _{e}a=a^{x}\ln a.}
Pasekmė . Jeigu
y
=
e
x
{\displaystyle y=e^{x}}
y
′
=
(
e
x
)
′
=
e
x
ln
e
=
e
x
.
{\displaystyle y'=(e^{x})'=e^{x}\ln e=e^{x}.}
[ keisti ] Jeigu funkcijos u ir v diferencijuojamos taške
x
0
,
{\displaystyle x_{0},}
tai jų sandauga diferencijuojama šiame taške ir
(
u
v
)
′
=
u
′
v
+
u
v
′
{\displaystyle (uv)'=u'v+uv'}
(funkcijų ir jų išvestinių reikšmės apskaičiuojamos taške
x
0
{\displaystyle x_{0}}
Iš pradžių apskaičiuosime sandaugos pokytį:
Δ
(
u
v
)
=
u
(
x
0
+
Δ
x
)
v
(
x
0
+
Δ
x
)
−
u
(
x
0
)
v
(
x
0
)
=
{\displaystyle \Delta (uv)=u(x_{0}+\Delta x)v(x_{0}+\Delta x)-u(x_{0})v(x_{0})=}
=
(
u
(
x
0
)
+
Δ
u
)
(
v
(
x
0
)
+
Δ
v
)
−
u
(
x
0
)
v
(
x
0
)
=
{\displaystyle =(u(x_{0})+\Delta u)(v(x_{0})+\Delta v)-u(x_{0})v(x_{0})=}
=
u
(
x
0
)
v
(
x
0
)
+
Δ
u
v
(
x
0
)
+
u
(
x
0
)
⋅
Δ
v
+
Δ
u
Δ
v
−
u
(
x
0
)
v
(
x
0
)
=
{\displaystyle =u(x_{0})v(x_{0})+\Delta uv(x_{0})+u(x_{0})\cdot \Delta v+\Delta u\Delta v-u(x_{0})v(x_{0})=}
=
Δ
u
v
(
x
0
)
+
u
(
x
0
)
Δ
v
+
Δ
u
Δ
v
.
{\displaystyle =\Delta uv(x_{0})+u(x_{0})\Delta v+\Delta u\Delta v.}
Iš čia
Δ
(
u
v
)
Δ
x
=
Δ
u
Δ
x
v
(
x
0
)
+
u
(
x
0
)
Δ
v
Δ
x
+
Δ
u
Δ
v
Δ
x
.
{\displaystyle {\frac {\Delta (uv)}{\Delta x}}={\frac {\Delta u}{\Delta x}}v(x_{0})+u(x_{0}){\frac {\Delta v}{\Delta x}}+\Delta u{\frac {\Delta v}{\Delta x}}.}
Kadangi funkcijos u ir v yra diferencijuojamos taške
x
0
,
{\displaystyle x_{0},}
Δ
u
Δ
x
→
u
′
;
Δ
v
Δ
x
→
v
′
;
Δ
u
→
0
,
{\displaystyle {\frac {\Delta u}{\Delta x}}\to u';\;\;{\frac {\Delta v}{\Delta x}}\to v';\;\;\Delta u\to 0,}
kai
Δ
x
→
0.
{\displaystyle \Delta x\to 0.}
Todėl
Δ
(
u
v
)
Δ
x
→
u
′
v
(
x
0
)
+
u
(
x
0
)
v
′
+
0
v
′
=
{\displaystyle {\frac {\Delta (uv)}{\Delta x}}\to u'v(x_{0})+u(x_{0})v'+0v'=}
=
u
′
v
(
x
0
)
+
u
(
x
0
)
v
′
,
{\displaystyle =u'v(x_{0})+u(x_{0})v',\;}
(
u
v
)
′
=
u
′
v
+
u
v
′
.
{\displaystyle \;(uv)'=u'v+uv'.}
Tai ir reikėjo įrodyti.
Jeigu funkcijos u ir v diferencijuojamos taške
x
0
{\displaystyle x_{0}}
ir funkcijos v reikšmė nelygi nuliui šiame taške, tai dalmuo
u
v
{\displaystyle {\frac {u}{v}}}
taip pat diferencijuojamas taške
x
0
{\displaystyle x_{0}}
ir
(
u
v
)
′
=
u
′
v
−
u
v
′
v
2
{\displaystyle \left({\frac {u}{v}}\right)'={\frac {u'v-uv'}{v^{2}}}}
(funkcijų ir jų išvestinių reikšmės apskaičiuojamos taške
x
0
{\displaystyle x_{0}}
Iš pradžių išvesime formulę
(
1
v
)
′
=
−
v
′
v
2
.
{\displaystyle \left({\frac {1}{v}}\right)'=-{\frac {v'}{v^{2}}}.}
Tam tikslui rasime funkcijos
1
v
{\displaystyle {\frac {1}{v}}}
Δ
(
1
v
)
=
1
v
(
x
0
+
Δ
x
)
−
1
v
(
x
0
)
=
v
(
x
0
)
−
v
(
x
0
+
Δ
x
)
v
(
x
0
)
v
(
x
0
+
Δ
x
)
=
−
Δ
v
v
(
x
0
)
(
v
(
x
0
)
+
Δ
v
)
.
{\displaystyle \Delta \left({\frac {1}{v}}\right)={\frac {1}{v(x_{0}+\Delta x)}}-{\frac {1}{v(x_{0})}}={\frac {v(x_{0})-v(x_{0}+\Delta x)}{v(x_{0})v(x_{0}+\Delta x)}}={\frac {-\Delta v}{v(x_{0})(v(x_{0})+\Delta v)}}.}
Iš čia
Δ
(
1
v
)
Δ
x
=
−
Δ
v
Δ
x
v
(
x
0
)
(
v
(
x
0
)
+
Δ
v
)
.
{\displaystyle {\frac {\Delta \left({\frac {1}{v}}\right)}{\Delta x}}={\frac {-{\frac {\Delta v}{\Delta x}}}{v(x_{0})(v(x_{0})+\Delta v)}}.}
Jei
Δ
x
→
0
,
{\displaystyle \Delta x\to 0,}
Δ
v
Δ
x
→
v
′
{\displaystyle {\frac {\Delta v}{\Delta x}}\to v'}
v diferencijuojama taške
x
0
{\displaystyle x_{0}}
Δ
v
→
0.
{\displaystyle \Delta v\to 0.}
Δ
(
1
v
)
Δ
x
=
−
v
′
v
⋅
v
=
−
v
′
v
2
,
{\displaystyle {\frac {\Delta \left({\frac {1}{v}}\right)}{\Delta x}}={\frac {-v'}{v\cdot v}}=-{\frac {v'}{v^{2}}},\;}
(
1
v
)
′
=
−
v
′
v
2
;
{\displaystyle \;\left({\frac {1}{v}}\right)'=-{\frac {v'}{v^{2}}};}
čia dešinėse lygybių pusėse trumpumo dėlei rašoma
v
(
x
0
)
=
v
.
{\displaystyle v(x_{0})=v.}
Dabar, remdamiesi funkcijų sandaugos išvestinės skaičiavimo taisykle, randame dalmens išvestinę:
(
u
v
)
′
=
(
u
⋅
1
v
)
′
=
u
′
⋅
1
v
+
u
⋅
(
1
v
)
′
=
u
′
v
+
u
⋅
−
v
′
v
2
=
u
′
v
−
u
v
′
v
2
.
{\displaystyle \left({\frac {u}{v}}\right)'=\left(u\cdot {\frac {1}{v}}\right)'=u'\cdot {\frac {1}{v}}+u\cdot \left({\frac {1}{v}}\right)'={\frac {u'}{v}}+u\cdot {\frac {-v'}{v^{2}}}={\frac {u'v-uv'}{v^{2}}}.}
[ keisti ] Jeigu
f
(
x
)
=
y
=
u
v
,
{\displaystyle f(x)=y={\frac {u}{v}},}
f
′
(
x
)
=
y
′
=
u
′
v
−
u
v
′
v
2
.
{\displaystyle f'(x)=y'={\frac {u'v-uv'}{v^{2}}}.}
Įrodymas . Jeigu
Δ
y
{\displaystyle \Delta y}
Δ
u
{\displaystyle \Delta u}
Δ
v
{\displaystyle \Delta v}
y , u ir v , atitinkanti priaugimui
Δ
x
{\displaystyle \Delta x}
f
(
x
+
Δ
x
)
=
y
+
Δ
y
=
u
+
Δ
u
v
+
Δ
v
,
{\displaystyle f(x+\Delta x)=y+\Delta y={\frac {u+\Delta u}{v+\Delta v}},}
f
(
x
+
Δ
x
)
−
f
(
x
)
=
Δ
y
=
u
+
Δ
u
v
+
Δ
v
−
u
v
=
u
v
+
Δ
u
v
−
u
v
−
u
Δ
v
v
(
v
+
Δ
v
)
=
Δ
u
v
−
u
Δ
v
v
(
v
+
Δ
v
)
,
{\displaystyle f(x+\Delta x)-f(x)=\Delta y={\frac {u+\Delta u}{v+\Delta v}}-{\frac {u}{v}}={\frac {uv+\Delta uv-uv-u\Delta v}{v(v+\Delta v)}}={\frac {\Delta uv-u\Delta v}{v(v+\Delta v)}},}
Δ
y
Δ
x
=
Δ
u
v
−
u
Δ
v
Δ
x
v
(
v
+
Δ
v
)
=
Δ
u
Δ
x
v
−
u
Δ
v
Δ
x
v
(
v
+
Δ
v
)
,
{\displaystyle {\frac {\Delta y}{\Delta x}}={\frac {\frac {\Delta uv-u\Delta v}{\Delta x}}{v(v+\Delta v)}}={\frac {{\frac {\Delta u}{\Delta x}}v-u{\frac {\Delta v}{\Delta x}}}{v(v+\Delta v)}},}
f
′
(
x
)
=
y
′
=
lim
Δ
x
→
0
Δ
y
Δ
x
=
lim
Δ
x
→
0
Δ
u
Δ
x
v
−
u
Δ
v
Δ
x
v
(
v
+
Δ
v
)
=
v
lim
Δ
x
→
0
Δ
u
Δ
x
−
u
lim
Δ
x
→
0
Δ
v
Δ
x
v
lim
Δ
x
→
0
(
v
+
Δ
v
)
.
{\displaystyle f'(x)=y'=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}=\lim _{\Delta x\to 0}{\frac {{\frac {\Delta u}{\Delta x}}v-u{\frac {\Delta v}{\Delta x}}}{v(v+\Delta v)}}={\frac {v\lim _{\Delta x\to 0}{\frac {\Delta u}{\Delta x}}-u\lim _{\Delta x\to 0}{\frac {\Delta v}{\Delta x}}}{v\lim _{\Delta x\to 0}(v+\Delta v)}}.}
Iš čia, pastebėję, kad
Δ
v
→
0
{\displaystyle \Delta v\to 0}
Δ
x
→
0
{\displaystyle \Delta x\to 0}
lim
Δ
x
→
0
Δ
v
=
0
,
{\displaystyle \lim _{\Delta x\to 0}\Delta v=0,}
v(x) - diferencijuojama ir dėl to netrūki funkcija), gauname:
f
′
(
x
)
=
y
′
=
u
′
v
−
u
v
′
v
2
.
{\displaystyle f'(x)=y'={\frac {u'v-uv'}{v^{2}}}.}
[ keisti ] Sudetine rodikline funkcija vadinasi funkcija, kurios pagrindas ir laipsnio rodiklis yra funkcijos nuo x , pavyzdžiui
(
sin
x
)
x
2
,
x
tan
x
,
x
x
,
(
ln
x
)
x
,
{\displaystyle (\sin x)^{x^{2}},\;x^{\tan x},\;x^{x},\;(\ln x)^{x},\;}
y
=
[
u
(
x
)
]
v
(
x
)
=
u
v
{\displaystyle y=[u(x)]^{v(x)}=u^{v}}
yra sudetinė rodiklinė funkcija (dažnai tokią funkciją vadina laipsnine rodikline funkcija). Jeigu
y
=
u
v
,
{\displaystyle y=u^{v},}
y
′
=
v
u
v
−
1
u
′
+
u
v
v
′
ln
u
.
{\displaystyle y'=vu^{v-1}u'+u^{v}v'\ln u.}
Įrodymas . Logaritmuojame funkciją y :
ln
y
=
v
ln
u
.
{\displaystyle \ln y=v\ln u.}
Diferencijuodami gautą lygybę per x , turėsime:
1
y
y
′
=
v
1
u
u
′
+
v
′
ln
u
,
{\displaystyle {\frac {1}{y}}y'=v{\frac {1}{u}}u'+v'\ln u,}
Iš kur
y
′
=
y
(
v
u
′
u
+
v
′
ln
u
)
.
{\displaystyle y'=y(v{\frac {u'}{u}}+v'\ln u).}
Įstatę čia išraišką
y
=
u
v
,
{\displaystyle y=u^{v},}
y
′
=
u
v
(
v
u
′
u
+
v
′
ln
u
)
=
v
u
v
−
1
u
′
+
u
v
v
′
ln
u
.
{\displaystyle y'=u^{v}(v{\frac {u'}{u}}+v'\ln u)=vu^{v-1}u'+u^{v}v'\ln u.}
Pavyzdžiai. Jeigu
y
=
x
x
,
{\displaystyle y=x^{x},}
y
′
=
x
x
x
−
1
(
x
′
)
+
x
x
(
x
′
)
ln
x
=
x
x
+
x
x
ln
x
=
x
x
(
1
+
ln
x
)
.
{\displaystyle y'=xx^{x-1}(x')+x^{x}(x')\ln x=x^{x}+x^{x}\ln x=x^{x}(1+\ln x).}
Jeigu
y
=
(
sin
x
)
x
2
,
{\displaystyle y=(\sin x)^{x^{2}},}
y
′
=
x
2
(
sin
x
)
x
2
−
1
(
sin
x
)
′
+
(
sin
x
)
x
2
(
x
2
)
′
ln
sin
x
=
{\displaystyle y'=x^{2}(\sin x)^{x^{2}-1}(\sin x)'+(\sin x)^{x^{2}}(x^{2})'\ln \sin x=}
=
x
2
(
sin
x
)
x
2
−
1
cos
x
+
(
sin
x
)
x
2
2
x
ln
sin
x
.
{\displaystyle =x^{2}(\sin x)^{x^{2}-1}\cos x+(\sin x)^{x^{2}}2x\ln \sin x.}
[ keisti ] Išvestinė funkcijos
y
=
x
α
{\displaystyle y=x^{\alpha }\;}
α
{\displaystyle \alpha }
y
′
=
α
x
α
−
1
.
{\displaystyle y'=\alpha x^{\alpha -1}.}
Įrodymas . Kadangi
y
=
x
α
,
{\displaystyle y=x^{\alpha },}
ln
y
=
ln
x
α
,
{\displaystyle \ln y=\ln x^{\alpha },}
ln
y
=
α
ln
x
.
{\displaystyle \ln y=\alpha \ln x.}
Diferencijuodami (remdamiesi sudėtinės funkcijos diferencijavimu) per x kairiąją ir dešiniąją puses, randame
(
ln
y
)
′
=
(
α
ln
x
)
′
,
{\displaystyle (\ln y)'=(\alpha \ln x)',}
y
′
y
=
α
x
,
{\displaystyle {\frac {y'}{y}}={\frac {\alpha }{x}},}
y
′
=
y
α
x
=
x
α
α
x
=
α
x
α
−
1
.
{\displaystyle y'=y{\frac {\alpha }{x}}=x^{\alpha }{\frac {\alpha }{x}}=\alpha x^{\alpha -1}.}
[ keisti ] Sudėtinės funkcijos
y
(
t
)
=
f
(
x
)
=
f
(
ϕ
(
t
)
)
{\displaystyle y(t)=f(x)=f(\phi (t))}
x
=
ϕ
(
t
)
{\displaystyle x=\phi (t)}
y
′
(
t
)
=
f
′
(
x
)
⋅
ϕ
′
(
t
)
.
{\displaystyle y'(t)=f'(x)\cdot \phi '(t).}
Kadangi nėra sudėtinės funkcijos išvestinės aiškiai suprantamo įrodymo, tai mes įrodysime, remdamiesi sudėtinės funkcijos išvestinės formule, per pavyzdį.
Tegu turime funkciją
y
=
t
15
=
(
t
3
)
5
;
{\displaystyle y=t^{15}=(t^{3})^{5};}
f
(
x
)
=
x
5
,
{\displaystyle f(x)=x^{5},}
x
=
ϕ
(
t
)
=
t
3
.
{\displaystyle x=\phi (t)=t^{3}.}
Surandame y , f(x) ir
ϕ
(
t
)
{\displaystyle \phi (t)}
y
′
=
(
t
15
)
′
=
15
t
14
,
{\displaystyle y'=(t^{15})'=15t^{14},}
f
′
(
x
)
=
(
x
5
)
′
=
5
x
4
,
{\displaystyle f'(x)=(x^{5})'=5x^{4},}
ϕ
′
(
t
)
=
(
t
3
)
′
=
3
t
2
.
{\displaystyle \phi '(t)=(t^{3})'=3t^{2}.}
Įstatę į f(x) išvestinę
x
=
t
3
{\displaystyle x=t^{3}}
ϕ
(
t
)
{\displaystyle \phi (t)}
y
′
=
f
′
(
x
)
⋅
ϕ
′
(
t
)
=
5
(
t
3
)
4
⋅
3
t
2
=
5
t
12
⋅
3
t
2
=
15
t
14
.
{\displaystyle y'=f'(x)\cdot \phi '(t)=5(t^{3})^{4}\cdot 3t^{2}=5t^{12}\cdot 3t^{2}=15t^{14}.}
Skaičiuojant abiais būdais gavome tą patį y išvestinės atsakymą (
y
′
=
15
t
14
{\displaystyle y'=15t^{14}}
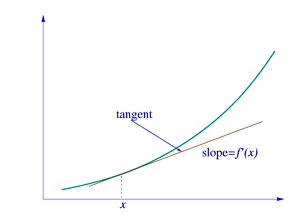
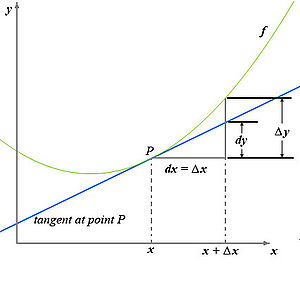



















































![{\displaystyle \Delta y-dy=[2x_{0}\Delta x+(\Delta x)^{2}]-[(6(x_{0}+\Delta x)-9)-x_{0}^{2}]=7-6=1,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15e98546ec9b0eae3d7d0ce3ef6e42ec7c0f5ad1)
![{\displaystyle \Delta y-dy=[f(x_{0}+\Delta x)-f(x_{0})]-[y(x_{0}+\Delta x)-f(x_{0})]=7-6=1,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c41a3027148aef00acd7f69d976bcc0597f4f5a1)
![{\displaystyle \Delta y-dy=[f(x_{0}+\Delta x)-f(x_{0})]-[f'(x_{0})\cdot \Delta x]=[2\cdot x_{0}\cdot \Delta x+(\Delta x)^{2}]-[2\cdot x_{0}\cdot \Delta x]=(\Delta x)^{2}=1^{2}=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad30fce870e3c6cd0494276d3d6423ce45cdfbb7)



















































































![{\displaystyle {\frac {\Delta y}{\Delta x}}={\frac {1}{\Delta x}}\log _{a}\left(1+{\frac {\Delta x}{x}}\right)={\frac {1}{x}}\cdot {\frac {x}{\Delta x}}\cdot \log _{a}\left(1+{\frac {\Delta x}{x}}\right)={\frac {1}{x}}\log _{a}\left[\left(1+{\frac {\Delta x}{x}}\right)^{\frac {x}{\Delta x}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5bef000da41ed0e222823ed05ea074627d0342c)


![{\displaystyle y'=\lim _{\Delta x\to 0}{\frac {\Delta y}{\Delta x}}={\frac {1}{x}}\log _{a}\left[\left(1+{\frac {\Delta x}{x}}\right)^{\frac {x}{\Delta x}}\right]={\frac {1}{x}}\log _{a}{\text{e}}={\frac {1}{x\ln a}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8181904e77c2fe05a2c3ec74dc8dfb78f3b6af88)







































































































![{\displaystyle y=[u(x)]^{v(x)}=u^{v}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c0506f4b4e72d185d0913c7ae42d83252df482c)
































